Мембранная теория
Страница 1

Давайте же посмотрим, сначала чисто качественно, как объясняется этой теорией возникновение биопотенциалов.

Что было важно для Бернштейна в строении органов и клеток? Мышца или нерв состоят из клеток, окруженных межклеточной жидкостью. Каждая клетка представляет собой мешочек или пузырек, покрытый оболочкой и содержащий жидкость другого состава.

Оболочка клетки — это и есть мембрана. Она отделяет клетки не друг от друга, а внутреннюю среду клетки от внешней межклеточной среды.

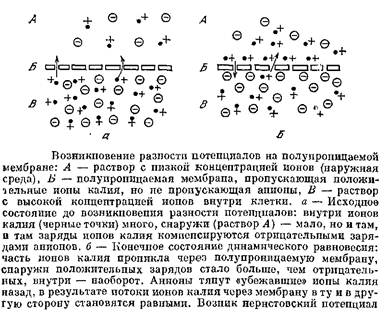
Пусть теперь внутри клетки имеется много свободных ионов какого-то элемента, например калия, а снаружи таких ионов нет или их гораздо меньше. Пусть клеточная мембрана пропускает только ионы К+ и не пропускает никаких других ионов. Тогда ионы К+ начнут выходить из клетки, где их много, наружу. Вместе с ними будет выноситься наружу их положительный заряд. Внутрь через мембрану будет проходить мало ионов, так как снаружи мало калия. В результате на клеточной мембране будет возникать разность потенциалов: снаружи клетки — «плюс», а внутри — «минус». Эта разность потенциалов будет тормозить движение новых положительных заряженных ионов калия наружу, и увеличивать поток этих ионов внутрь. Когда потоки ионов наружу и внутрь сравняются, установится динамическое равновесие и на мембране будет поддерживаться постоянная разность потенциалов. Это и есть потенциал покоя. Его величина описывается формулой Нернста.

Чтобы вывести эту формулу, воспользуемся тем, что согласно теории растворов Вант-Гоффа переход ионов из раствора с большей концентрацией С2 в раствор с меньшей концентрацией Сх представляет собой как бы расширение «ионного газа»: если в растворе с концентрацией С2 некоторое количество ионов занимает объем V2, то в растворе с концентрацией Сг они займут объем Vlt причем C1V1= СгУг. При этом меняется внутренняя анергия ионного газа, которая и переходит в потенциальную энергию зарядов, равную qE, где q — заряд, а Е — возникшая разность потенциалов.

Так как изменение внутренней энергии газа определяется только его начальным и конечным состояниями и не зависит от того, каким способом произошел переход из одного состояния в другое, попробуем найти изменение энергии в самом простом случае — когда при расширении газа совершается механическая работа.

Пусть у нас есть цилиндр с газом, закрытый поршнем, и пусть газ, расширяясь, движет поршень, совершая работу, равную произведению силы на путь: А = FI. Сила равна произведению давления газа на площадь поршня, т. е. А = PSI. Но произведение площади на перемещение есть изменение объема газа. Следовательно, изменение энергии газа при расширении определяется формулой AW=PаV.

Если бы давление Р при расширении, т. е. при изменении объема, не менялось, то работа была бы равна произведению Р, т. е. площади прямоугольника ABCD. Но из уравнения газового состояния RT = PV следует, что с увеличением объема давление падает по закону Р = ЯТ/У. Значит, при постоянной температуре Т работа расширения одного моля газа от Уг до У2 равна площади криволинейной трапеции под гиперболой и может быть вычислена по формуле

А так как концентрация газа обратно пропорциональна объему, то У2 = сУС2 и А = ИТ 1п.

Страницы: 1 2 3 4


Другие статьи:

Пожизненная долговременная память
Все приведенные положения, касающиеся изменения состояния некоторых белков и моделируемые, в частности, с помощью долговременной синаптической потенциации нейронов гиппокампа, касаются лишь относительно кратковременных процессов, сопостав ...

Пища, приготовленная природой
Молоко— идеальный продукт питания. Павлов писал, что среди других видов человеческой еды особое место отведено молоку. Это «пища, приготовленная самой природой». Она входит в рацион всех цивилизованных народов с древнейших времен. Археол ...

Чем отличается естественнонаучный подход от философского? Какова дисциплинарная структура естествознания, как она сложилась и как менялась? Каковы критерии истинности знания? Что такое «научная карт
Естествознание исследует органическую и неорганическую природу на Земле и во вселенной. Специфика естествознание заключается в том, что знание о природе отличается объективностью, постоянно совершенствуется и представляет собой наиболее д ...