Уравнение электродиффузии ионов через мембрану в приближении однородного поля
Рассмотрим перенос заряженных частиц (ионов). В отсутствие градиента концентрации главная движущая сила при переносе ионов - электрическое поле. Если частица (ион) в водном растворе или внутри мембраны находится во внешнем электрическом поле с градиентом потенциала 
, то она будет двигаться. Соблюдение Ома для таких систем означает, что между скоростью движения частицы "u" и действующей силой 
имеется линейная зависимость:
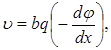
где q - заряд частицы, b - подвижность носителя заряда (иона). Переходя к плотности тока j = qnu, где n - число частиц в единице объема, получаем в направлении оси "X":
.
Поток частиц "Ф" равен потоку электричества "j", деленному на заряд каждой частицы "q", то есть
(1)
Выразим "Ф" как функцию градиента термодинамического потенциала, так как q = ze (e - заряд электрона), таким образом, согласно E = z F(j2 - j1 ), где E - энергия электрического поля, F - число Фарадея, z - заряд иона.
F = NA e, E = z e NA(j2 - j1) = qNA(j2 - j1),
тогда
, (G - свободная энергия), (2)
где NA - число Авогардо.
Сопоставив (1) и (2), получаем:
где 
- молярная концентрация частиц (Кмоль/м ).
Это уравнение соблюдается и для явлений диффузии, и для электрофореза в однородном растворителе.
Теорелл (1954 г.) обобщил это выражение для случая, когда изменяется не только концентрация вещества "с" и потенциал "j", но и химическое сродство иона к окружающей среде "m0" (в частности, к растворителю). Тогда уравнение потока принимает следующий вид (уравнение Теорелла):
(3)
где 
- электрохимический потенциал. То есть поток равен произведению концентрации носителя на его подвижность и на градиент его электрохимического потенциала. Знак "-" указывает на то, что поток направлен в сторону убывания .
Для однородной среды 
и учитывая значение 
, подставленное в (3) получается электродиффузное уравнение Нернста - Планка:
где R - универсальная газовая постоянная, T - абсолютная температура.
Другие статьи:
Глотание
После того, как сформировался пищевой комок, происходит глотание. Это рефлекторный процесс, в котором выделяют три фазы:
· ротовую (произвольную и непроизвольную);
· глоточную (быструю непроизвольную);
· пищеводную (медленную непроизво ...
Уход за лошадью
Родина лошади - просторы степей. Всё время в стойле держать её нельзя. Для того чтобы лошадь хорошо себя чувствовала, ей просто необходимо ежедневно много двигаться. Такие условия существуют только в сельской местности, где лошади светлое ...
Механизмы вкуса
Описание механизмов вкуса и запаха часто объединяют, потому что оба ощущения активируются химическими стимулами, приходящими из внешнего мира. Действительно, некоторые вкусовые стимулы действуют на G-протеин сопряженные рецепторы способам ...